ReLU 也能“万能近似”？用「黎曼积分 + 拼积木」把它讲透

很多人第一次听到万能近似定理（Universal Approximation Theorem，UAT）时，会下意识把它和 Sigmoid / Tanh 这种 S 型函数绑定在一起，于是就会产生一个疑问：

ReLU 这么“直来直去”的折线激活函数，真的也能逼近任意函数吗？

答案是：能。而且理解它的方式非常朴素——就像用积木拼出任意形状一样。

什么是「万能近似定理」？

维基百科

通俗说法是：

在人工神经网络的数学理论中，万能近似定理指出：神经网络有能力近似任意函数（在一定条件下），并且可以达到任意精度。
但它也明确了一个“坑”：它不告诉你怎么选参数（权重、神经元数量、层数等）才能近似到你想要的目标函数——它更多是一个“存在性证明”。

历史脉络：

1989 年，乔治·西本科（Cybenko）证明：单隐藏层、任意宽度，并使用 S 型函数作为激活函数的前馈网络，具有通用逼近能力。
1991 年，Kurt Hornik 证明：激活函数的选择不是关键，前馈网络的多层结构与多神经元架构，才是其成为通用逼近器的关键之一。

ReLU 为啥也行？

理解 ReLU 的万能近似，你只需要抓住一个关键词：

矩形逼近法（把复杂曲线用很多“小块”拼起来）

可以借用微积分里 **黎曼积分（Riemann Integral）**的直觉来类比：

构建积木：单个神经元（尤其是 ReLU）是简单的“折线块”。把多个 ReLU 经过平移、缩放、翻转后叠加，就能做出像“凸起/方块/梯形”一样的局部结构。
拼凑曲线：任何复杂的连续曲线，都可以看作由无数个足够窄的“矩形”（或局部小块）拼起来。
无限逼近：
- 每一个“小矩形/小块”，对应一组神经元的组合；
- 神经元足够多 ⇒ 小块足够多；
- 调整每个小块的高度和位置（本质就是调 w 和 b）⇒ 就能把目标函数越拼越像，精度任你要。

一句话：只要基础材料足够简单、数量足够多，就能拼出任意复杂形态。

直接上手：用 ReLU 翻转叠加做「梯形函数」和「三角函数」

下面这部分是理解的“爽点”：你会看到 ReLU 怎么像搭积木一样搭出形状。

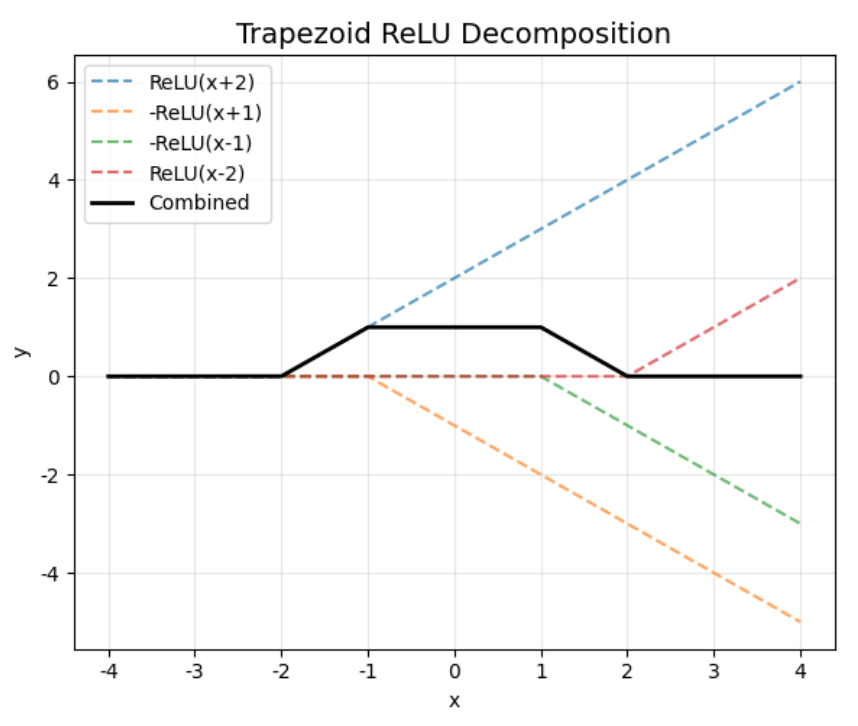
梯形函数（Trapezoid）

形状示意：

1
2
3
4
5


形状:         ___________
             /           \
            /             \
      _____/               \_____
          a    b     c     d

用 ReLU 组合出梯形的一种写法（原文公式）：

公式：

1

f(x) = h/(b-a) × [ReLU(x-a) - ReLU(x-b) - ReLU(x-c) + ReLU(x-d)]

直觉理解：

ReLU(x-a) 从 a 开始往上爬；
-ReLU(x-b) 让它在 b 之后“别再继续爬”（形成平台/拐点）；
再叠加 -ReLU(x-c) + ReLU(x-d)，让右侧出现对称的下坡并在 d 后归零；
系数 h/(b-a) 控制整体高度比例。

你可以把它当作：用 4 个“折线斜坡”拼出一个梯形凸起。

三角函数（Triangle）

形状示意：

1
2
3
4
5


形状:           /\
              /  \
             /    \
      _____/       \_____
          a   b   c

用 ReLU 组合出三角的一种写法（原文公式）：

公式：

1

f(x) = k1×ReLU(x-a) - (k1+k2)×ReLU(x-b) + k2×ReLU(x-c)

其中：

k1 = h/(b-a)
k2 = h/(c-b)

直觉理解：

a 到 b：由 k1×ReLU(x-a) 主导上升；
b 之后：用 -(k1+k2)×ReLU(x-b) 把“上升趋势”掰回来；
c 之后：用 +k2×ReLU(x-c) 把尾部校正到合适的形态。

代码/Notebook

notebook地址

为什么这就足够解释「万能近似」？

当你能用 ReLU 组合出任意位置、任意高度、任意宽度的“梯形/三角/小凸起”时：

把一条连续曲线切成很多很多小段；
每小段用一个（或一组）小凸起去拟合；
小段越细、凸起越多 ⇒ 误差就越小；
极限意义下，你就得到了“可以任意逼近”的结论。

这甚至比“傅里叶变换里用无数正弦叠加逼近任何连续曲线”更好直观：

本质上殊途同归：只要我有足够多简单的基础材料（波浪或方块），我就能重构出世界上任何复杂的形态。